Geometric Deep Learning
Generative Adversarial Net
Gudmundur Einarsson
Technical University of Denmark
Technical University of Denmark
October 3rd 2018
GANs, a very hot topic!

Points I want to try to address
What is a GAN?
What are the challenges using GANs? E.g. learning
Examples of applications
Why is it interesting for us!
Check out iangoodfellow.com for nice presentations
What is the problem GANs solve?
GANs are a way to create very good generative models
They properly model the data manifold
- Achieved by using an adversary
- Learns to discriminate between real and generated samples
- Pushes generator to become better
Let’s see the difference
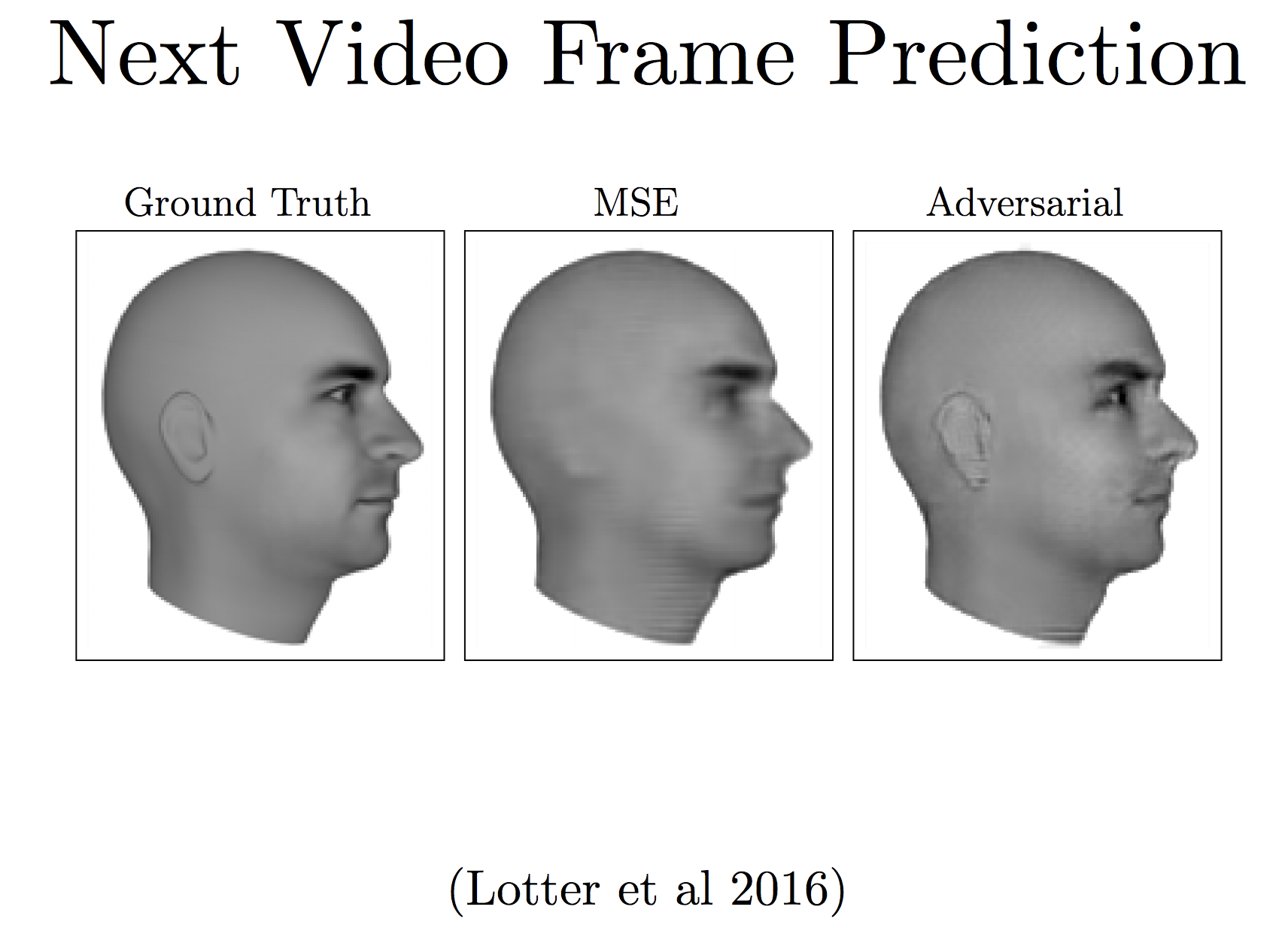
Why the hype?

Named GANs
There are around 500 new GAN paper every month
Check out the GAN model zoo on github for inspiration
This is simply too much material to cover
Focus and stick to the original paper
If time, look at ganerated hands, as an example application
The GAN paper
- Basic GAN idea
- Game between generator \(G\) and Discriminator \(D\)
- Both are generic, in original papers are MLPs
- This generic part is one of the reason for popularity
- \(D\) is a differentiable function which discriminates real and generated data, has parameters \(\boldsymbol{\theta}^{(D)}\)
- \(\mathbf{x}\) is the input
- \(D(\mathbf{x})\) is the probability of sample being real
- Has cost function \(J^{(D)}(\boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)})\)
- \(G\) is a differentiable function, has parameters \(\boldsymbol{\theta}^{(G)}\)
- \(\mathbf{z}\) sample from some prior
- \(G(\mathbf{z})\) gives an \(\mathbf{x}\) from \(p_{\text{model}}\)
- \(\mathbf{z}\) is very flexible, can inject noise in many places
- Has cost function \(J^{(G)}(\boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)})\)
- Has cost function \(J^{(G)}(\boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)})\)
How do we train these?
Multiple different approaches
- Simultaneous SGD
- Minibatch from of \(\mathbf{x}\) values from dataset
- Minibatch of \(\mathbf{z}\) value from model prior
- Take simultaneous gradient steps
- update \(\boldsymbol{\theta}^{(D)}\) to reduce \(J^{(D)}\)
- update \(\boldsymbol{\theta}^{(G)}\) to reduce \(J^{(G)}\)
Can use any gradient base optimization, e.g. Adam
Cost function for \(D\)
\[ J^{(D)}(\boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)}) = -\frac{1}{2}\mathbb{E}_{\mathbf{x}\sim p_{\text{data}}}\log D(\mathbf{x}) -\frac{1}{2}\mathbb{E}_{\mathbf{z}}\log (1- D(G(\mathbf{z}))) \]
This is standard cross-entropy for binary classifier with a sigmoid output
- Trained with two minibatches of data
- One from dataset, the ones
- One generated, the zeroes
Cost function for \(G\)
Here are more choices, simplest is the zero-zum game \[ J^{(G)} = -J^{(D)} \]
This allows us to summarize all into one value function \[ V\left( \boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)} \right) = -J^{(D)}\left( \boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)} \right) \]
This allows us solve a minimax proble, which is the solution to zero-sum games \[ \boldsymbol{\theta}^{(G)*} = \text{arg} \min_{\boldsymbol{\theta}^{(G)}}\max_{\boldsymbol{\theta}^{(D)}}V\left( \boldsymbol{\theta}^{(D)},\boldsymbol{\theta}^{(G)} \right) \]
Mostly interesting for theoretical analysis
Practical problems and other cost functions
If the discriminator becomes too good, then gradient for the generator vanishes. It gets stuck and we do not see any improvements.
Heuristic change, flip target to construct in stead of sign \[ J^{(G)} = -\frac{1}{2}\mathbb{E}_{\mathbf{z}}\log D(G(\mathbf{z})) \]
Generator now maximizes the probability of the discriminator being wrong, instead of minimizing the probability of the discriminator being correct.
Can no longer use one single value function
DCGANs
- Radford et. al 2015
- Deep convolution GANs
- Three new key insights
- Batch normalization, in both \(G\) and \(D\), normalize the two minibatches seperately
- Based on the all-convolutional net (Springenberg et. al 2015), for increasing spatial dimension we use transposed convolution with stride greater than 1.
- They use Adam instead of SGD with momentum.
Tips and tricks
- Train with labels
- Make the discriminator recognize specific classes of objects
- One-sided label smoothing
- Change the ones to \(0.9\)
- Virtual batch normalization
- Use a reference batch, sample at beginning, and current batch to estimate normalization values.
- Otherwise the two different minibatches cause too much fluctuation in the normalization parameters.
- In practice, \(D\) is usually deeper, more filters per layer
Example use case, CVPR 2018

Whole Pipeline
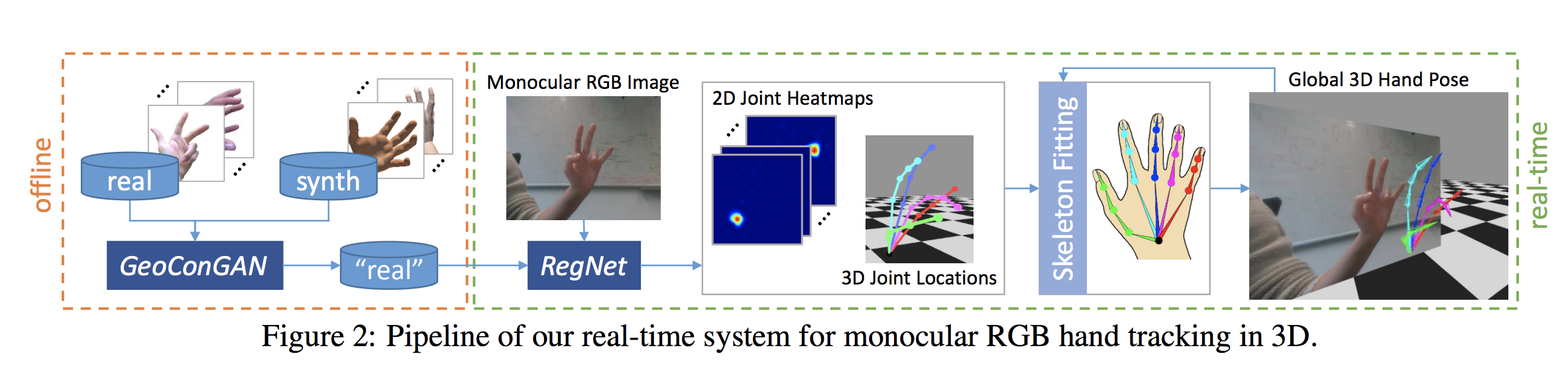
GeoConGan
Image to image translation network
Translate synthetic images to realistic looking images
We have ground truth annotations for synthetic data, they just don’t look real enough
Generating realistic hands

Geometric Consistency, important for consistent annotations

See in action
What do the authors release?
Implementation in caffe
Heatmaps are 128 by 128
Only release forward pass for tracking
Issues for GANs
GANs are not the holy grail of deep learning
They have some very hard problems to solve
Issues, how to evaluate performance?
Samples from LARGE SCALE GAN TRAINING FOR HIGH FIDELITY NATURAL IMAGE SYNTHESIS

Are these just look ups from the training data?

Are these just look ups from the training data?

Are these just look-ups from the training data?

Future paper to look into
More examples where gans are used to synthesize training data
Cycle gans, maybe info GAN
Focus on more high resolution image generation