Geometric Deep Learning
(Introduction) & Applications
Gudmundur Einarsson
Technical University of Denmark
July 10th 2018
Who am I
- From Iceland, live in Denmark
- Postdoc at DTU Compute focusing on geometric deep learning (GDL)
- Image Analysis & Computer Graphics Group
- PhD in Applied Mathematics defended in April 2018
- Focus on Statistical Learning, in particular sparse classification
- During the summer at deCODE genetics here in Iceland
Collaborators in GDL
- Rasmsus R. Paulsen
- Line K. H. Clemmensen
- Others in reading group (geo-dl.compute.dtu.dk)
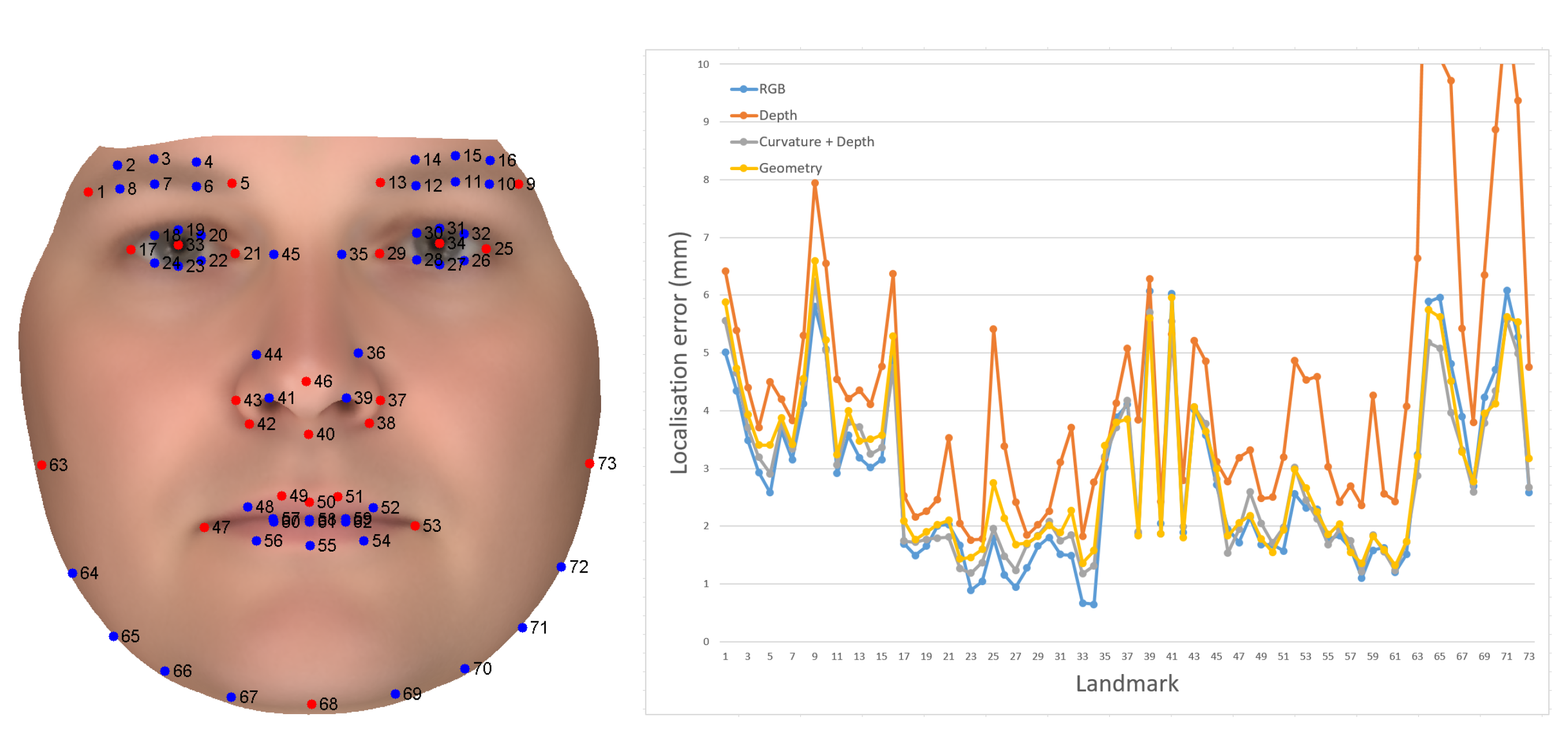
Prediction of Facial Landmarks
- We are interested in modeling the external anatomy of face and ear
- Used for accoustic simulations for optimal placements of microphones for hearing aids
- Accurate landmarks for phenotyping (what is a phenotype?)
- GDL caught our attention
Outline
- What is geometric about GDL?
- Why do we need GDL?
- Different Data, Different Problems and Different Approaches
- Preliminary Results for landmark prediction on faces
- Deep Learning and Genetics
What does geometric mean?
What do we refer to as geometric?
- Geometry is associated with the data, compared to images, which provide a single view and can be regarded as a euclidean grid
- Different input data
- 3D-point clouds, e.g. from 3D scans
- Volumetric data, Discritization of meshes or medical scans
- Meshes, e.g. Computer Aided Design drawings or Computer Graphics objects
- Usually surfaces embedded in 3D
- Non-euclidean geometries, how to calculate distances?
- Other graph structures, e.g. social networks or epidemiological networks.
3D point clouds
 Stanford Bunny Point Cloud
Stanford Bunny Point Cloud
Volumetric data
 Stanford Bunny Volumetric
Stanford Bunny Volumetric
Meshes
 Stanford Bunny Mesh
Stanford Bunny Mesh
What are the applications?
- Classification
- Big catalogues of CAD models
- Segmentation
- Semantic segmentation and scene segmentation
- Dense & Sparse point correspondances
- Landmark annotations
- Shape analysis
Why do we need DL on this?
- Better and faster methods for e.g. classification
- Challenges in generalization to input for DL methods
- We want improvements similar to image and text based problems
- Meet the increase in acquisition of 3D data
- Scanning of museaum artifacts
- 3D-face and body scans
- Archeology scans
- Quality assurance in factories, real time scanning is on the way
Structured Light Scanning
 Scanning of Polar Bear Skulls
Scanning of Polar Bear Skulls
Different Approaches for Different Data
Different Approaches for Different Data
- Different represenations of data call for different approaches
- Different problems to tackle!
- We need invariances to different properties of the data, e.g.:
- Point Clouds should be invariant to permutations of the individual points
- Volumetric data should be invariant of orientation
- Meshes should be invariant to changes in triangulation of faces
Point Clouds Example Approaches
Point Clouds Example Approaches
- PointNet and PointNet++ from Stanford
- Implemented for 3D classification and segmentation
- Each point is treated independently as a 3d point in the input
PointNet Requirements
- Unordered, invariant to the N! permutations of the input
- Interaction Among Points, need to capture combinatorial interactions in local structures
- Invariance Under Transformations, rotation and translation should not affect our predictions/classifications
Strategies for learning with unordered data
- Sort input in canonical order
- No ordering is stable in high dimensional space for point perturbations
- Treat input as a sequence for an RNN and permute training data
- Hard to scale for long sequences, works for N=10-100, point clouds usually have at least 1000 points (usually way more)
- Simple symmetric functions for information aggregation
PointNet Idea
- Approximate a general function on a pointset by applying a symmetric function on transformed elements in the set \[
f(\{ x_1,...,x_n \}) \approx g(h(x_1),...,h(x_n))
\]
- \(f\) takes in a set, so it is invariant to permutations
- \(h\) is a multi-layer percepteron
- \(g\) is a composition of a single variable function and max pooling
- With several differnt \(h\) functions we can create a global descriptor of the point cloud
- Global descriptors are used for classification
Other Details for PointNet
- Affine transformation is predicted for canonical alignment
- Also applied to features deeper
- Semantic segmentation
- Feed global descriptors to points
- Combine local and global features for point classification
- Theoretical justification for universal approximation to continuous set function
- Trained on ModelNet40, 12k man-made CAD models from 40 categories
PointNet Architecture
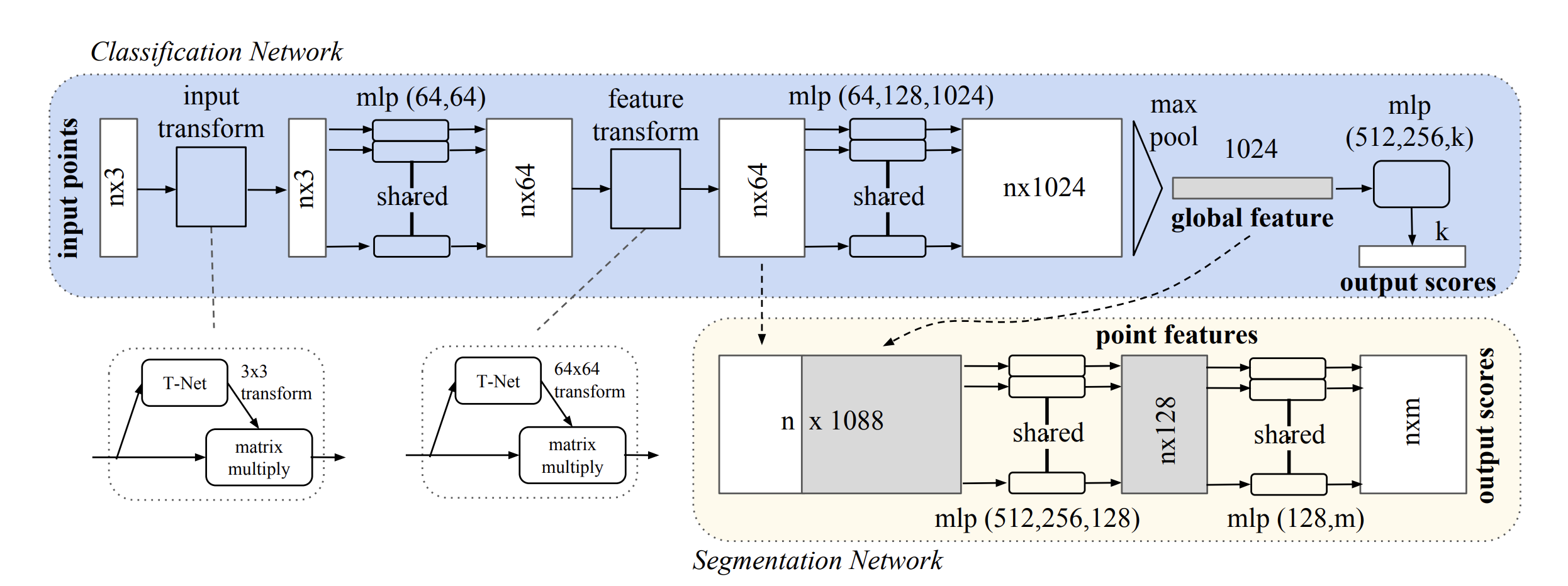 PointNet Architecture
PointNet Architecture
PointNet Results Kinect Left, CAD Right
 Results from PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
Results from PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
Volumetric and Multi-View Example Approaches
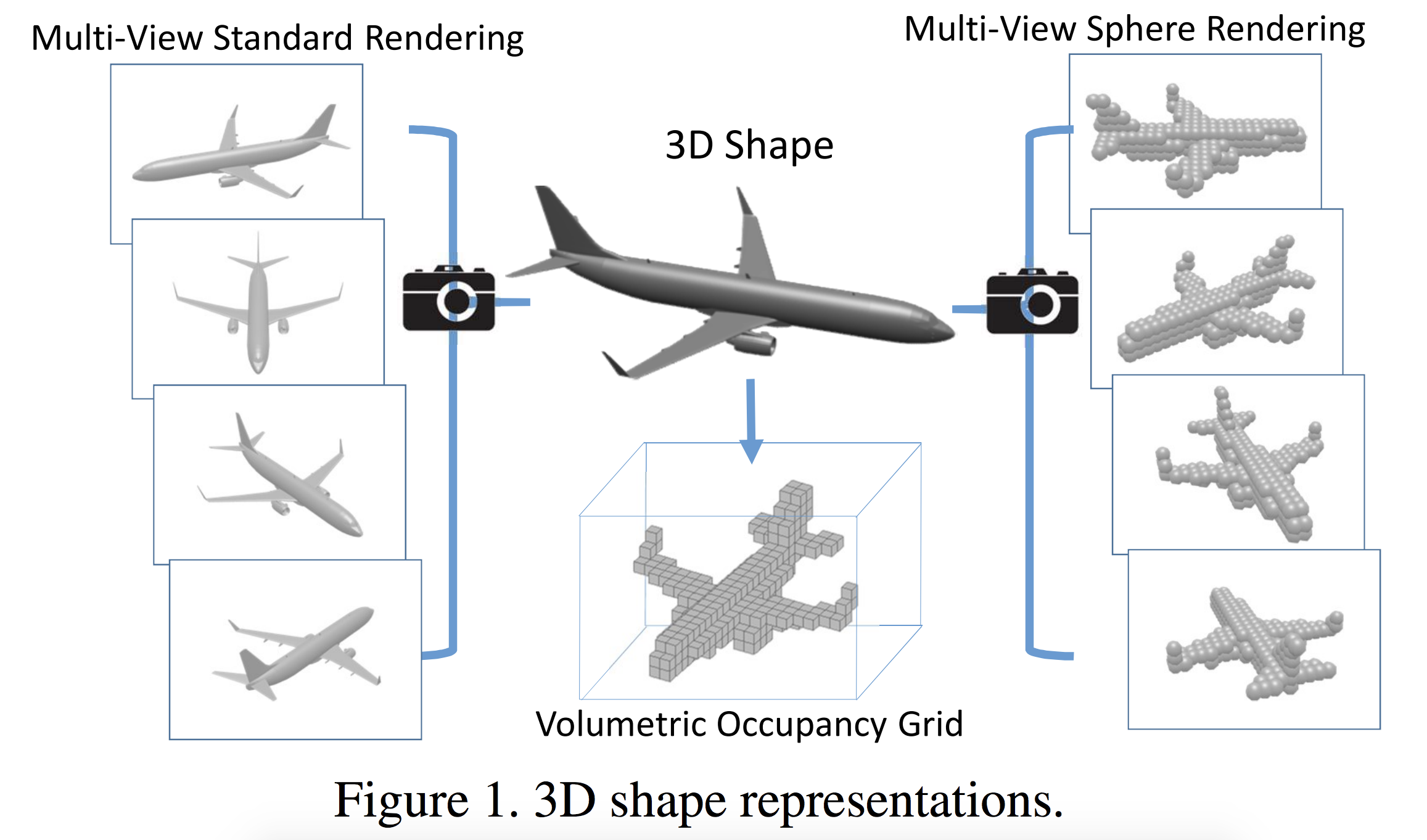 Results from Volumetric and Multi-View CNNs for Object Classification on 3D Data
Results from Volumetric and Multi-View CNNs for Object Classification on 3D Data
Main Ideas for Volumetric and Multi-View Approaches
- Auxiliary tasks
- Predict labels from subvolumes
- Helps to prevent overfitting
- Data augmentation
- Multi-Orientation Pooling
- Layer which aggregates information from many different views
- Also, multi-view pooling
Changing Voxel Resolution for Rendering and Volumetric Approaches
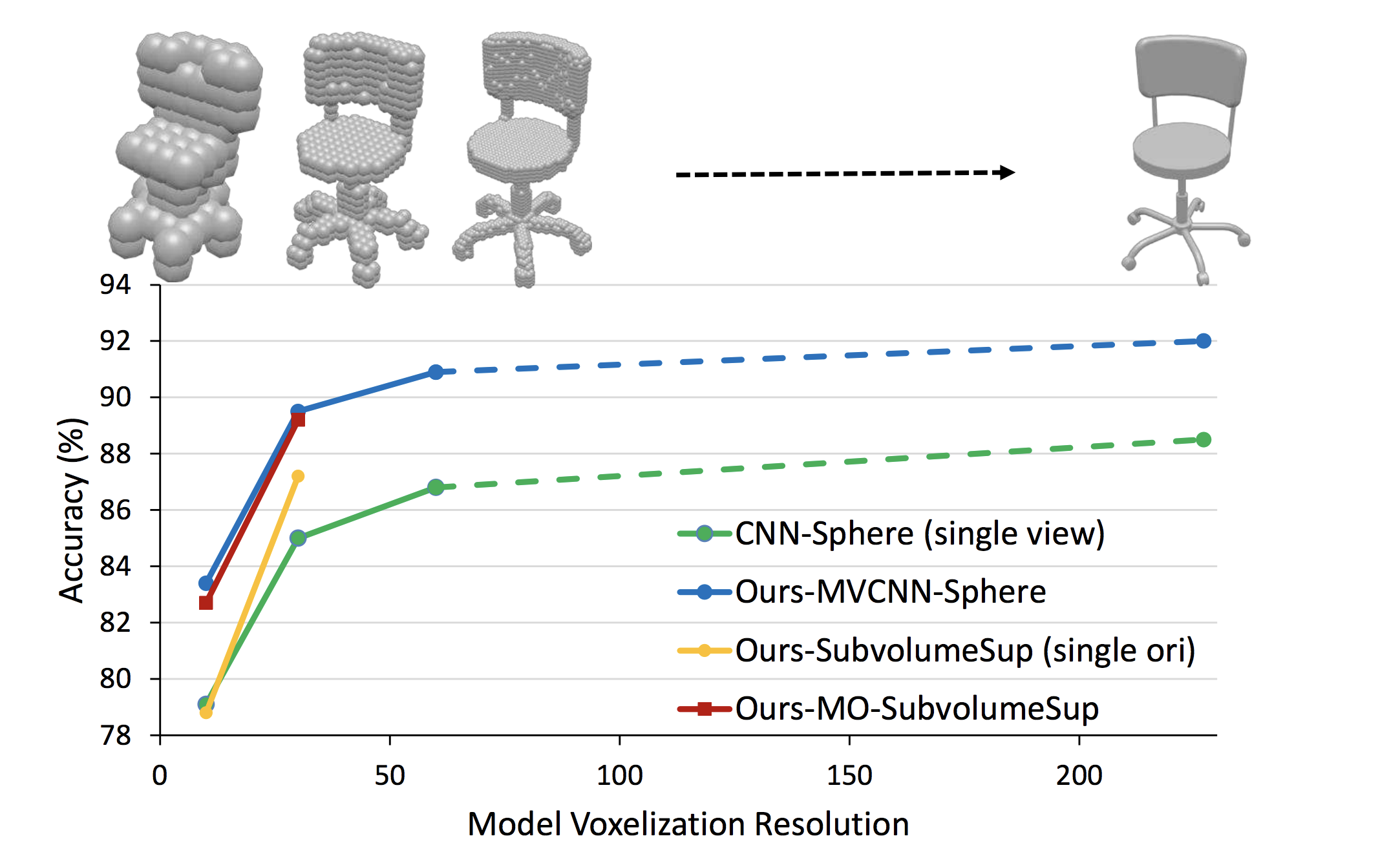 Results from Volumetric and Multi-View CNNs for Object Classification on 3D Data
Results from Volumetric and Multi-View CNNs for Object Classification on 3D Data
Invariance to isometry
- For point correspondances between two meshes, e.g. two scanned humans
- We need an intrinsic operator which only depends on the Riemannian metric of the manifold.
- Bronstein et. al propose the Laplace Beltrami Operator (LBO)
- LBO admits an eigendecomposition on a smooth compact manifold
- Generalization of Fourier series to non-Euclidean domains
- Allows for defining convolution on meshes
Decomposition is global
 Function, filter, same filter different mesh
Function, filter, same filter different mesh
Solved With Loacalised Approaches
 Different Localised Approaches
Different Localised Approaches
Back to Landmark Annotations
Our Pipeline
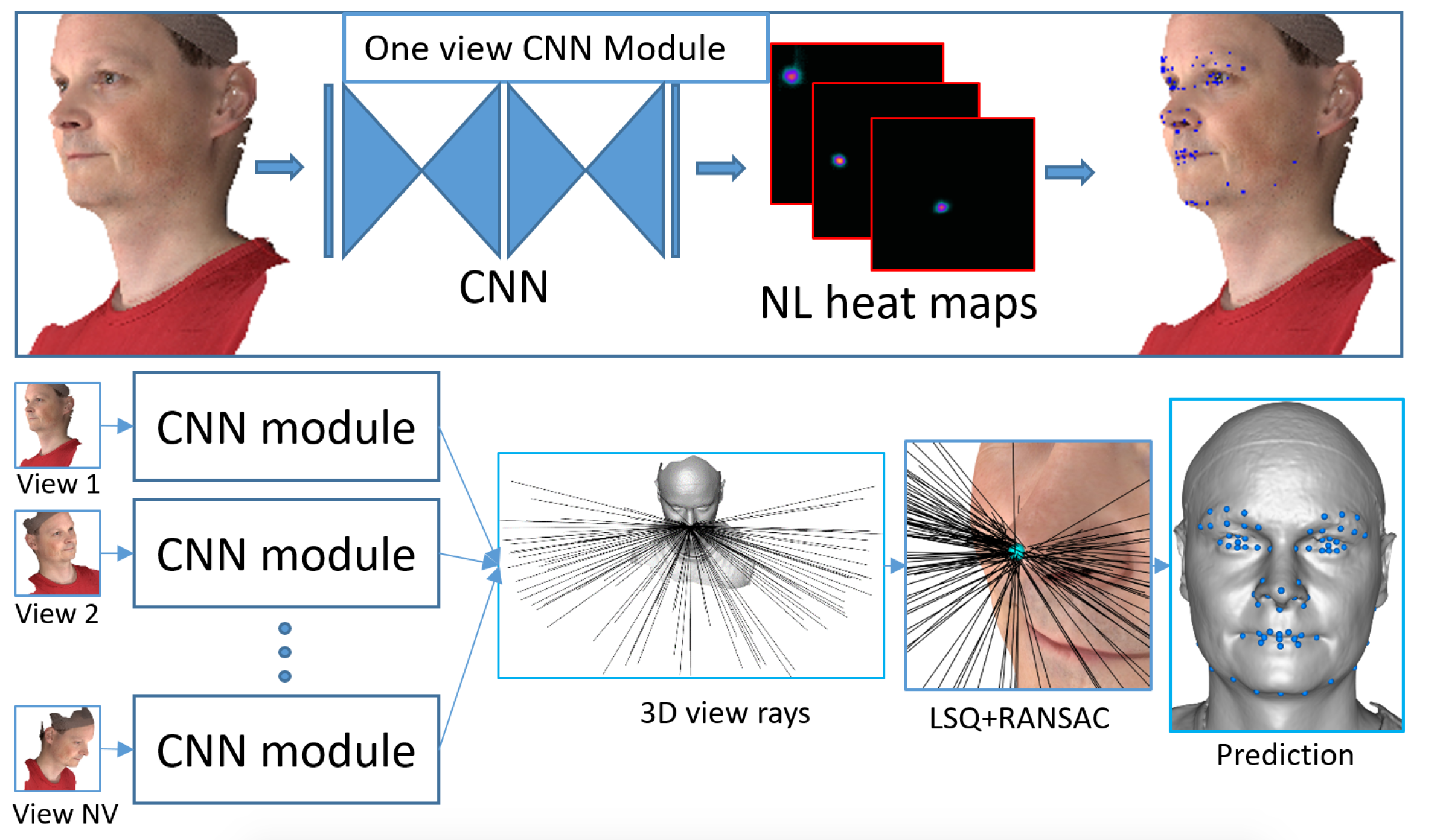 Two stacked hourglass networks
Two stacked hourglass networks
Applications to MRI
 Not restricted to 3D scans of faces
Not restricted to 3D scans of faces
Applications for Genetics (if time allows)
- Data-driven phenotypes (e.g. Big Five)
- Phenotypes from images
- Modern social phenotypes
Leaders in the Field
These individuals have paved the way in collaboration with their research groups.
- Professor Leonidas Guibas, Stanford
- Innovated approaches to volumetric and point-cloud data
- Professor Michael Bronstein, University of Lugano & Intel perceptual computing
- Convolution on meshes and dense mesh correspondances
Material for those interested
- Geometric Deep Learning SIGGRAPH ASIA 2016 course notes
- Geometric Deep Learning Webpage
- geo-dl.compute.dtu.dk, our reading group
Thanks Questions?
- Let me know if you come to Denmark!